Have you ever wondered how to find the shortest path between vertices on mesh? I have. Here’s the code.
I have recently decided to update few of my custom Maya tools from MEL to API. The most useful one, Planarize Edge Tool, was frankensteined from ZenTools, which contains all sort of useful functions for working with vertices. Now that I moved to C++, I had to come up with my own solution for finding the shortest path between multiple vertices. Before I could do that, I needed to cover a simple two-point scenario.
Shortest path between two vertices
Lets say we have even square mesh and vertices A and B. Since all edges have the same length (weight), the shortest path between vertices A and B will be the one with least iterations. In the following example it is four. In every iteration the path grafts to all connected points, increasing the search radius until the end vertex is reached.
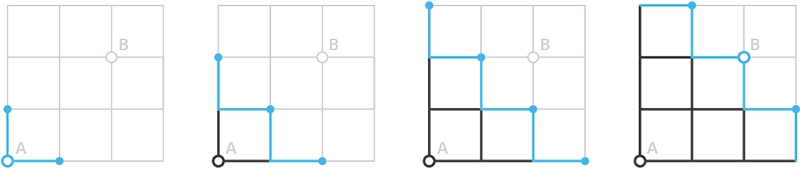
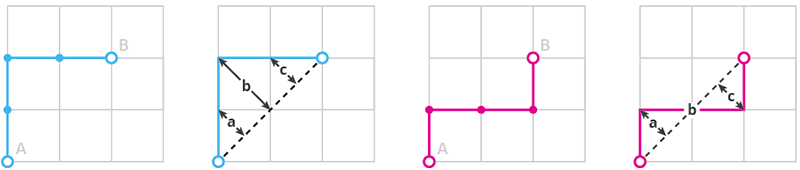
As you probably noticed, this method itself does’t produce a single path, rather a whole tree. To narrow it down we have to apply some rule. Following illustration shows two paths, both are results of the previous example. By measuring deviation of each path from a straight line between the two end-vertices, we can figure out which one is the most “direct” path. As you can see total deviation (a+b+c) is smaller with the second path. The deciding factor could be actually anything – corner angle, edge length, vertex index or color.
Implementation
We begin by initializing the storage variables and by extracting the base mesh and the end vertices from active selection.
|
1 2 3 4 5 6 7 8 9 10 11 |
MDagPath m_path; MStringArray m_pointPath; MDoublePath m_pathDev; int iterCounter; // Get info about selected mesh and vertices MSelectionList selectionList; status = MGlobal::getActiveSelectionList(selectionList, true); MObject component; status = selectionList.getDagPath(0, m_path, component); |
Now we have to convert the vertex data in correct format. For certain operations we’ll use vertices in form of a component object, in other cases it is easier to work with vertex indices in numeric format.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
// Extracting vertices from component MIntArray indices; MFnSingleIndexedComponent componentFn(component); status = componentFn.getElements(indices) MFnSingleIndexedComponent startVertexFn(); startVertex.create(MFn::kMeshVertComponent, &status); startVertexFn.addElement(indices[0]); // Finally calling the main function MString shortestPath; status = extendPath(startVertexFn.object(), indices[0], indices[1], shortestPath); |
‘Inception’
The extendPath function does all the magic thanks to MItMeshVertex::getConnectedVertices() method, which lists point on the other side of each edge connected to given vertex. In the first loop we call this function using the start point, in every next round it uses vertices collected in the previous iteration. This repeats until we reach the target vertex. It is a good idea to limit the number of iterations to number of all mesh vertices, to prevent infinite loop. Notice how we use the path deviation to choose between multiple paths pointing to the same vertex.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
inline MStatus extendPath(MObject& component, const int& start, const int& target, MString& path) { MStatus status(MStatus::kSuccess); MFnMesh meshFn(m_path, &status); // Iteration counter to prevent infinite loop iterCounter++; if( iterCounter >= meshFn.numVertices() ) return MStatus::kFailure; // This component will store vertices for next iteration MFnSingleIndexedComponent compList; compList.create(MFn::kMeshVertComponent, &status); MItMeshVertex vertexIt(m_path, component, &status); for (vertexIt.reset(); !vertexIt.isDone(); vertexIt.next()) { int parentIndex = vertexIt.index(); // Graft path to all connected vertices MIntArray connected; vertexIt.getConnectedVertices(connected); for (unsigned c = 0; c < connected.length(); c++) { int index = connected[c]; // Calculate deviation between path and direct line between end vetices MPoint first; MPoint parent; MPoint last; status = meshFn.getPoint(start, first, MSpace::kWorld); status = meshFn.getPoint(parentIndex, parent, MSpace::kWorld); status = meshFn.getPoint(target, last, MSpace::kWorld); double deviation = pointLineDistance(parent, first, last) + m_pathDev[parentIndex]; // In case we already have a shorter path to current vertex, ignore the new one if (deviation >= m_pathDev[index] && m_pointPath[index].numChars()>0) continue; // Extend path to current vertex m_pathDev[index] = deviation; m_pointPath[index] = m_pointPath[parentIndex] + parentIndex + ";"; // If we found the target vertex return the shortest path if (index == target) { path = m_pointPath[index]; return MStatus::kSuccess; } compList.addElement(index); } } // If we didn't find the end point, run another iteration using new vertex collection return extendPath(compList.object(), start, target, path); return MStatus::kFailure; } |
This function generates path in a string format containing vertex indices separated by semilocon e.g. “1;2;3;4;5;6”. For a bit more API friendly result use the following function to converted it into a numeric array.
|
1 2 3 4 5 6 7 8 9 10 11 |
inline MIntArray stringToIntArray(const MString& path) { MStringArray pathStrArray; path.split(';', pathStrArray); MIntArray pathIntArray; for (unsigned s = 0; s < pathStrArray.length(); s++) pathIntArray.append(pathStrArray[s].asInt()); return pathIntArray; } |
Conclusion
This fairly simple code is a great entry point for more complex solutions. By comparing paths generated by this method you can sort multiple vertices along an edge and find the shortest path between multiple vertices. Watch out for my future blog posts, it will definitely appear there.


2 Comments
Ravshan Gaziev
24 Apr 2022 - 1:17 pmYou can use just “polySelect” func. It will be much more short and faster
Stepan Jirka
25 Apr 2022 - 8:17 amHi Ravshan,
thank you for your suggestion – you might be right. I was looking for a solution that would work directly with C++ API without the need to call MEL or Python command.