In the first version of my Cross Sections I figured out how to find intersections between a mesh and a plane. After almost five months I finally found a way to sort these intersections so they can be used to create one or more curves.

In the previous version intersections were calculated for each edge of each polygonal face resulting in hundreds of line segments without any connection. This method wasn’t very efficitent. Every non-boundary edge has 2 adjacent faces, which means the program calculated almost twice as many intersections as necessary.

Finding intersections

The new algorithm is actually quite simple and has two phases. First intersections are calculated for individual edges of the mesh. Whenever the intersection is succesful the program stores edge ID, intersection point, parameter and whether the intersection lies on a boundary.

Then comes the second phase which sorts the intersections and creates one or more poly-lines. If there’s an intersection on a boundary, the iterator will make it the beginning of the new curve. In that case the result will be an opened section curve. If none of the intersections lies on a boundary, the first point in the intersection list will be used. In that case the points will form a closed curve.

Sorting intersections

In every iteration we first add the intersection to a curve CV list and remove it from the intersection list. This signals the edge has been already iterated (to avoid getting stuck in an infinite loop).

Now we list the adjacent faces of this edge and go through all edges connected to these faces checking for any match in the intersection list. Once the intersection is found another sortIntersections function is called for the new edge. When no more connections can be found, the iteration cycle is ended and a new degree 1 curve is created from the CV list.

This would only work in case none of the intersections lied on a vertex. That’s the reason why we stored the intersection parameter in the first place. Whenever the parameter equals 0 or 1, we list the adjacent faces of the edge vertex, instead of adjacent faces of the edge. Also once the next intersection is found, all the edges connected to this vertext have to be removed from the intersection list. Here’s a little example to make everything a bit clearer (or confusing).

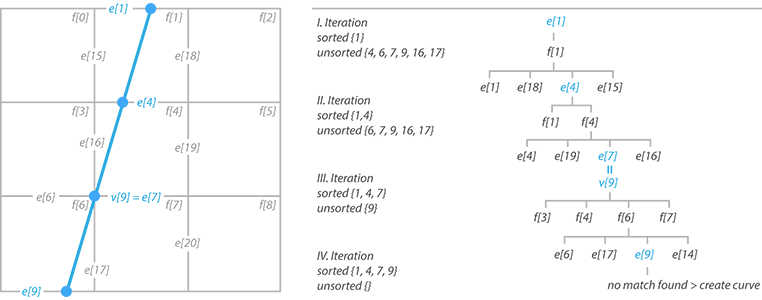
And here’s the sorting method in code. The 3 iterators – MItMeshPolygon, MItMeshEdge and MItMeshVertex – are passed as a parameter since initializing them inside the function every time was significantly decreasing performance.

Conclusion

Although in this case the sorting method deals with intersections between mesh and a plane, it can be used to sort intersection between mesh and any other geometry by simply changing the findIntersections function. Also don’t forget to check my github repository for the complete code.